Mersenne Asalları Üzerine Bir Karalama

Matematikle biraz içli-dışlı olanlarımız Mersenne adını mutlaka duymuşlardır.Tam adı Marin Marsenne olan bu Fransız matematikçi, genelde ünlü matematikçilerin babalarının yaptığı gibi, kilisede din adamı olmasını isteyen babasını dinlemeyip, Paris'e gider ve 60 yıllık hayatına (1588-1648) anlam kazandıracak şeylerle uğraşır.
Marsenne adı, kendi ismiyle anılan "Mersenne Asalları" ile anılır.Mersenne; p bir asal sayı iken, M=2^p - 1 şeklindeki tüm sayılarında asal olduğunu düşünmüştü...Gerçektende;

p=2=>M=3

p=3=>M=7

p=5=>M=31

p=7=>M=127

bir-iki deneme ile asal sayılar elde ediliyor...Fakat, bunu ispatlamak gerekiyordu...Acaba, her p asal sayısı için M bir asal sayımıydı?Matematiksel genellemeler üzerine yapılacak hatalardan bahsetmiştim.Denemelere devam edelim:

p=11=>M=2047=23.89...Hayal kırıklığı!!!

11 Mersenne için bir hayal kırıklığı yaratmadı, tabii...Çünkü, önermenin çift taraflı olmasa da yeter şartı doğruydu...Yani, M asal iken, p kesinlikle asaldı...Sayılarla biraz daha oynayalım...

p=13=>M=8191 de asaldır...

p=31=>M=2147483647 de asaldır...

p=101=>M=2535301200456458802993406410751=7432339208719.341117531003194129 asal değildir...Bu hesaplamaları Maple ile yaptım.

n=2, 3, 5, 7, 13, 17, 19, 31, 61, 89, için elde edilebilecek Mersenne asalları;

3, 7, 31, 127, 8191, 131071, 524287, 2147483647 dır.Grafiksel olarak Mersenne asallarının dağılımı aşağıdakine benzer:




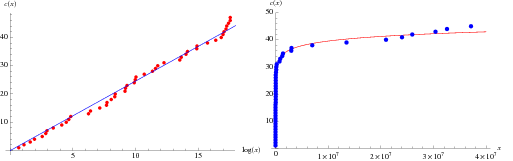
Matematikseverler hala Mersenne sayılarını elde etmek için uğraşıyorlar.Bunun için bilgisayarların yardımını alıyorlar doğal olarak...Acaba bilgisayarlar olmasa ne yapardık?Aşağıdaki tabloda bilinen ve bulanabilen Mersenne asallarını görebilirsiniz:

#		digits	year	discoverer (reference)	value
1	2	1	antiquity		3
2	3	1	antiquity		7
3	5	2	antiquity		31
4	7	3	antiquity		127
5	13	4	1461	Reguis (1536), Cataldi (1603)	8191
6	17	6	1588	Cataldi (1603)	131071
7	19	6	1588	Cataldi (1603)	524287
8	31	10	1750	Euler (1772)	2147483647
9	61	19	1883	Pervouchine (1883), Seelhoff (1886)	2305843009213693951
10	89	27	1911	Powers (1911)	618970019642690137449562111
11	107	33	1913	Powers (1914)	162259276829213363391578010288127
12	127	39	1876	Lucas (1876)	170141183460469231731687303715884105727
13	521	157	Jan. 30, 1952	Robinson (1954)	68647976601306097149...12574028291115057151
14	607	183	Jan. 30, 1952	Robinson (1954)	53113799281676709868...70835393219031728127
15	1279	386	Jun. 25, 1952	Robinson (1954)	10407932194664399081...20710555703168729087
16	2203	664	Oct. 7, 1952	Robinson (1954)	14759799152141802350...50419497686697771007
17	2281	687	Oct. 9, 1952	Robinson (1954)	44608755718375842957...64133172418132836351
18	3217	969	Sep. 8, 1957	Riesel	25911708601320262777...46160677362909315071
19	4253	1281	Nov. 3, 1961	Hurwitz	19079700752443907380...76034687815350484991
20	4423	1332	Nov. 3, 1961	Hurwitz	28554254222827961390...10231057902608580607
21	9689	2917	May 11, 1963	Gillies (1964)	47822027880546120295...18992696826225754111
22	9941	2993	May 16, 1963	Gillies (1964)	34608828249085121524...19426224883789463551
23	11213	3376	Jun. 2, 1963	Gillies (1964)	28141120136973731333...67391476087696392191
24	19937	6002	Mar. 4, 1971	Tuckerman (1971)	43154247973881626480...36741539030968041471
25	21701	6533	Oct. 30, 1978	Noll and Nickel (1980)	44867916611904333479...57410828353511882751
26	23209	6987	Feb. 9, 1979	Noll (Noll and Nickel 1980)	40287411577898877818...36743355523779264511
27	44497	13395	Apr. 8, 1979	Nelson and Slowinski	85450982430363380319...44867686961011228671
28	86243	25962	Sep. 25, 1982	Slowinski	53692799550275632152...99857021709433438207
29	110503	33265	Jan. 28, 1988	Colquitt and Welsh (1991)	52192831334175505976...69951621083465515007
30	132049	39751	Sep. 20, 1983	Slowinski	51274027626932072381...52138578455730061311
31	216091	65050	Sep. 6, 1985	Slowinski	74609310306466134368...91336204103815528447
32	756839	227832	Feb. 19, 1992	Slowinski and Gage	17413590682008709732...02603793328544677887
33	859433	258716	Jan. 10, 1994	Slowinski and Gage	12949812560420764966...02414267243500142591
34	1257787	378632	Sep. 3, 1996	Slowinski and Gage	41224577362142867472...31257188976089366527
35	1398269	420921	Nov. 12, 1996	Joel Armengaud/GIMPS	81471756441257307514...85532025868451315711
36	2976221	895832	Aug. 24, 1997	Gordon Spence/GIMPS	62334007624857864988...76506256743729201151
37	3021377	909526	Jan. 27, 1998	Roland Clarkson/GIMPS	12741168303009336743...25422631973024694271
38	6972593	2098960	Jun. 1, 1999	Nayan Hajratwala/GIMPS	43707574412708137883...35366526142924193791
39	13466917	4053946	Nov. 14, 2001	Michael Cameron/GIMPS	92494773800670132224...30073855470256259071
40	20996011	6320430	Nov. 17, 2003	Michael Shafer/GIMPS	12597689545033010502...94714065762855682047
41?	24036583	7235733	May 15, 2004	Josh Findley/GIMPS	29941042940415717208...67436921882733969407
42?	25964951	7816230	Feb. 18, 2005	Martin Nowak/GIMPS	12216463006127794810...98933257280577077247
43?	30402457	9152052	Dec. 15, 2005	Curtis Cooper and Steven Boone/GIMPS	31541647561884608093...11134297411652943871
44?	32582657	9808358	Sep. 4, 2006	Curtis Cooper and Steven Boone/GIMPS	12457502601536945540...11752880154053967871
45?	37156667	11185272	Sep. 6, 2008	Hans-Michael Elvenich/GIMPS	20225440689097733553...21340265022308220927
46?	43112609	12978189	Aug. 23, 2008	Edson Smith/GIMPS	31647026933025592314...80022181166697152511

İnsanoğlunda keşfetme merakı oldukça, bu tabloya yeni Mersenne sayılarının katılacağı aşikar...